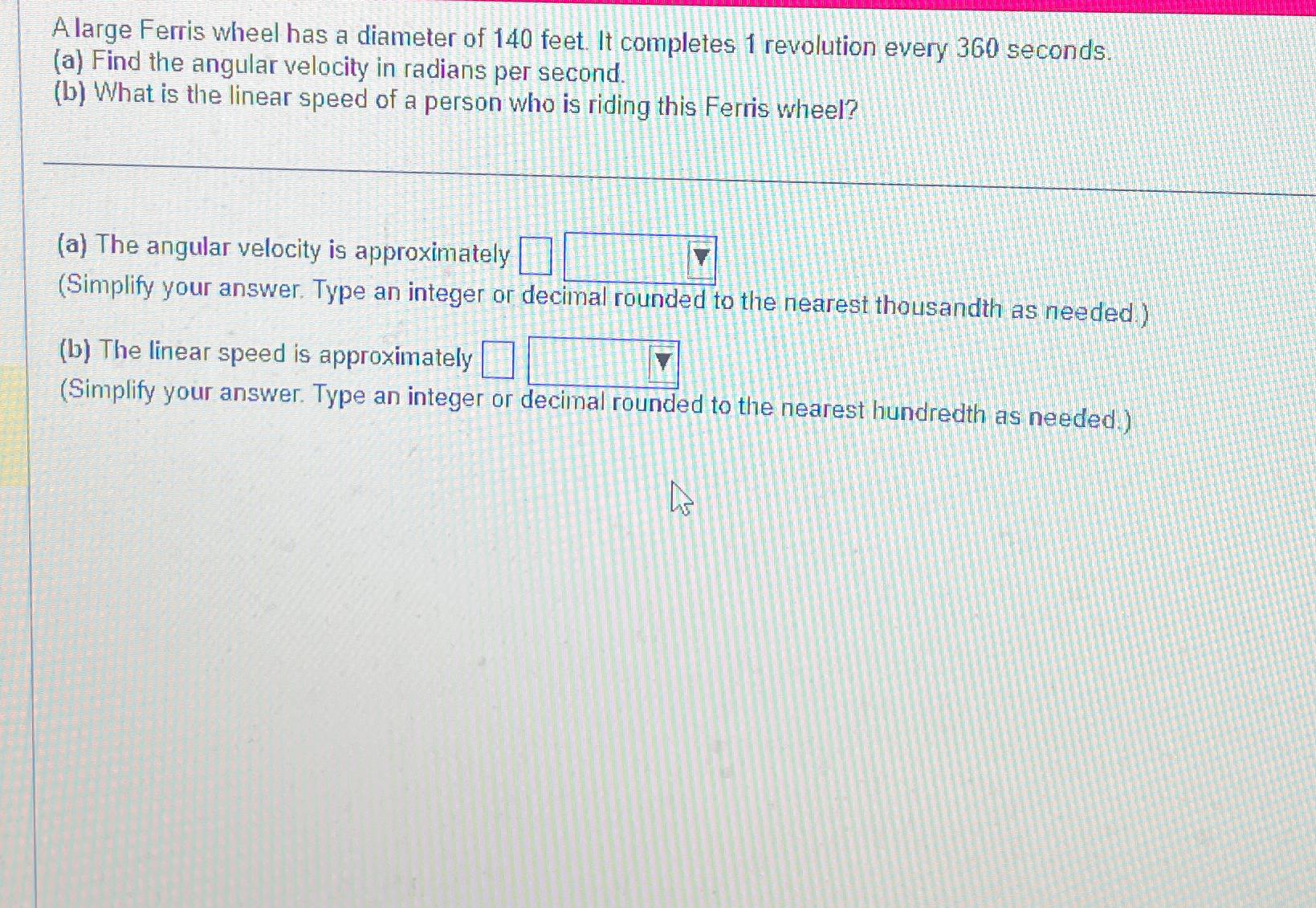
A Ferris wheel has a radius of 80 feet, a majestic structure that offers breathtaking views and a thrilling ride. This seemingly simple fact opens a door to a world of mathematical exploration, allowing us to delve into the fascinating geometry of circles and their real-world applications. From calculating the circumference and area of the wheel to understanding the relationship between its radius and the speed of its rotation, the Ferris wheel provides a tangible example of mathematical concepts in action.
By examining the Ferris wheel’s dimensions, we can gain a deeper appreciation for the interplay between mathematics and engineering. This exploration not only reveals the elegance of mathematical formulas but also highlights their practical significance in designing and constructing iconic structures like Ferris wheels.
Speed and Time
The exhilarating ride on a Ferris wheel is a blend of graceful movement and thrilling height. Understanding the speed at which a Ferris wheel rotates and the time it takes for a complete revolution is crucial to appreciating the mechanics of this iconic amusement park attraction.
Calculating Linear Speed
The linear speed of a passenger on a Ferris wheel is the distance traveled by the passenger in a given amount of time. To calculate the linear speed, we need to know the circumference of the Ferris wheel and the time it takes for one complete rotation.
- The circumference of a circle is given by the formula 2πr, where r is the radius. In this case, the radius of the Ferris wheel is 80 feet, so the circumference is 2π(80) = 160π feet.
- The time for one complete rotation is given as 2 minutes.
- Therefore, the linear speed of a passenger at the edge of the wheel is the circumference divided by the time: (160π feet) / (2 minutes) = 80π feet/minute ≈ 251.33 feet/minute.
Relationship Between Radius and Time
The radius of a Ferris wheel and the time it takes to complete one rotation are inversely proportional. This means that as the radius of the Ferris wheel increases, the time it takes for one rotation decreases, and vice versa.
- Consider two Ferris wheels, one with a radius of 40 feet and another with a radius of 80 feet. If both Ferris wheels complete one rotation in the same amount of time, the passenger on the Ferris wheel with a radius of 80 feet will travel a greater distance in the same amount of time, resulting in a higher linear speed.
- This inverse relationship can be explained by the fact that the circumference of a circle is directly proportional to its radius. As the radius increases, the circumference increases, requiring a faster rotation to complete one revolution in the same amount of time.
Visual Representation
To better understand the dimensions and features of the Ferris wheel, let’s visualize it through a simple diagram and a table that summarizes its key measurements.
Diagram of the Ferris Wheel
The diagram below illustrates the Ferris wheel with its radius, diameter, and circumference labeled:[Diagram description: A circle representing the Ferris wheel with a line extending from the center to the edge, labeled “Radius (80 feet)”. Another line passing through the center and connecting opposite points on the circle, labeled “Diameter (160 feet)”. A curved line along the edge of the circle, labeled “Circumference (502.65 feet)”.]
Ferris Wheel Dimensions
The following table provides a concise summary of the Ferris wheel’s dimensions:
| Dimension | Value (feet) |
|---|---|
| Radius | 80 |
| Diameter | 160 |
| Circumference | 502.65 |
| Area | 20,106.24 |
Applications of Circles
Circles are ubiquitous in our world, appearing in nature, architecture, engineering, and everyday objects. Their unique properties make them incredibly versatile, lending themselves to various applications and influencing numerous aspects of our lives.
Applications of Circles in Engineering and Design
Circular shapes offer distinct advantages in engineering and design, making them a preferred choice for numerous applications.
- Strength and Stability: Circles distribute forces evenly, resulting in structures that are strong and stable. This is evident in bridges, domes, and cylindrical structures, where the circular shape enhances their ability to withstand stress and pressure. For example, the Eiffel Tower, a testament to the strength and stability of circular structures, uses a latticework of interconnected triangles and circular elements to support its massive weight.
- Efficiency: Circular shapes optimize space and minimize material usage. In pipelines and pipes, circular cross-sections maximize the flow of liquids and gases while minimizing friction. This efficiency extends to gears and bearings, where circular teeth and surfaces ensure smooth and efficient movement with minimal wear and tear.
- Versatility: Circles can be easily adapted to various purposes. For example, wheels, a fundamental component of transportation, utilize circular shapes for smooth and efficient movement. In machinery, circular gears and bearings are crucial for transmitting power and facilitating motion.
Disadvantages of Circular Shapes in Design and Engineering, A ferris wheel has a radius of 80 feet
While circles offer significant advantages, there are also considerations regarding their limitations in design and engineering.
- Limited Flexibility: Unlike rectangular or triangular shapes, circles are less flexible and adaptable to complex geometries. This can pose challenges in designing structures with intricate shapes or incorporating curves and angles.
- Potential for Instability: While circles offer strength and stability, certain configurations can lead to instability. For instance, a thin circular plate can buckle under pressure, requiring additional support or reinforcement to maintain its structural integrity.
- Manufacturing Complexity: Creating precise circular shapes can be challenging and require specialized tools and techniques. This can increase manufacturing costs and complexity, particularly when dealing with large or intricate circular components.
The Ferris wheel, with its 80-foot radius, serves as a captivating illustration of how mathematical principles can be applied to real-world scenarios. From understanding the wheel’s circumference and area to calculating the speed of its rotation, we have explored the intricate relationship between geometry and engineering. This journey not only showcases the beauty of mathematics but also emphasizes its crucial role in shaping our world, one captivating structure at a time.
FAQs: A Ferris Wheel Has A Radius Of 80 Feet
How many people can fit on a Ferris wheel with an 80-foot radius?
The number of passengers a Ferris wheel can accommodate depends on its design, specifically the size and spacing of the gondolas. There’s no direct correlation between radius and passenger capacity.
What is the maximum height a person would reach on this Ferris wheel?
Assuming the Ferris wheel is anchored to the ground, the maximum height a person would reach is twice the radius, or 160 feet. This includes the height of the wheel itself and the additional height from the bottom of the gondola to the top.
How long would it take to complete one full rotation on this Ferris wheel?
The time it takes to complete one rotation depends on the Ferris wheel’s speed, which is not directly related to its radius. Some Ferris wheels rotate slowly, while others complete a rotation in a matter of seconds.