Imagine a wheel of radius r and negligible mass is mounted, a seemingly simple object, yet one that holds the key to understanding fundamental concepts in mechanics. This wheel, devoid of its own weight, becomes a fascinating subject for exploring the interplay of motion, forces, and energy. Its radius, a defining characteristic, directly influences its movement and potential energy, while its negligible mass allows us to focus on the pure mechanics of motion without the complexities of inertia.
The journey through this analysis reveals how a simple wheel can be a powerful tool for understanding the principles that govern the world around us.
This exploration delves into the types of motion the wheel can experience, from simple rotations to complex combinations of rotation and translation. We’ll examine the forces that act upon it, such as gravity, friction, and applied forces, and how these forces affect its motion. The relationship between the wheel’s radius, angular velocity, and linear velocity will be unveiled, showcasing how these interconnected quantities govern the wheel’s movement.
The Wheel’s Properties and Significance
The wheel, a seemingly simple invention, holds profound significance in the realm of physics and engineering. Its properties, particularly its negligible mass and radius, play crucial roles in determining its motion and potential energy. Understanding these properties allows us to analyze its behavior in various applications and scenarios.
The Significance of Negligible Mass
The assumption of negligible mass for the wheel simplifies the analysis of its motion. By neglecting the wheel’s mass, we can focus on the motion of the object it is attached to, without considering the wheel’s inertia or rotational kinetic energy. This simplification is valid in situations where the mass of the object is significantly larger than the mass of the wheel.
For instance, when analyzing the motion of a car, the mass of the wheels is typically negligible compared to the mass of the car itself.
The Implications of the Wheel’s Radius
The radius “r” of the wheel plays a crucial role in determining its motion and potential energy.
Relationship between Radius and Angular Velocity
The radius of the wheel is directly related to its angular velocity. When the wheel rotates, the linear velocity “v” of a point on the rim is related to the angular velocity “ω” by the equation:
v = rω
This relationship implies that a larger radius results in a higher linear velocity for the same angular velocity.
Relationship between Radius and Potential Energy
The radius of the wheel also influences its potential energy. When a wheel is raised to a certain height, its potential energy is determined by its mass and height. However, the radius of the wheel can affect the height to which it can be raised. For example, a wheel with a larger radius will require a greater height to reach the same potential energy as a wheel with a smaller radius.
Potential Applications and Scenarios
The wheel’s properties make it applicable in a wide range of scenarios.
Mechanical Systems
Wheels are fundamental components in various mechanical systems, including vehicles, machines, and rotating equipment. Their ability to translate rotational motion into linear motion makes them essential for transportation, power transmission, and material handling.
Energy Storage
Wheels can be used in energy storage systems. For example, flywheels, which are rotating wheels with a large moment of inertia, can store kinetic energy and release it when needed. This principle is utilized in energy storage applications such as grid stabilization and hybrid vehicles.
Scientific Research
Wheels play a crucial role in scientific research, particularly in experiments involving rotational motion. They are used in devices like centrifuges, which separate substances based on density, and gyroscopes, which maintain a fixed orientation.
Motion and Forces Acting on the Wheel: A Wheel Of Radius R And Negligible Mass Is Mounted
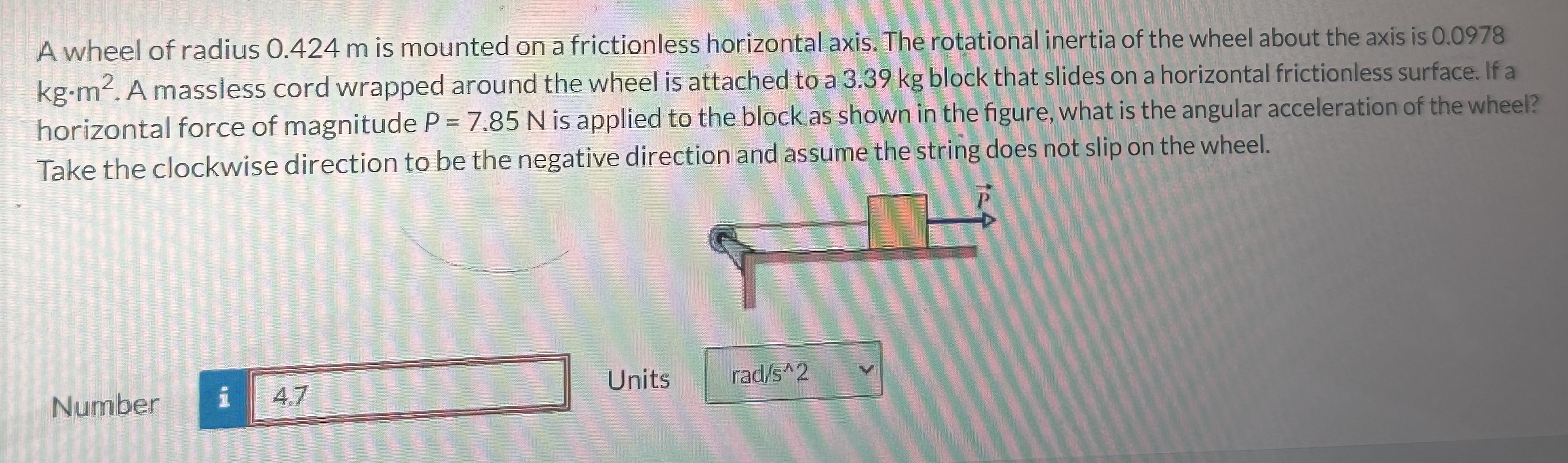
The motion of a wheel can be quite complex, depending on how it is being used. It can undergo both rotational and translational motion, or a combination of the two. The forces acting on the wheel will determine its motion and behavior.
Types of Motion
The types of motion a wheel can undergo depend on the forces acting on it and how it is supported. Here’s a breakdown:* Rotation: The wheel rotates around its axis, which is typically the center of the wheel. This is the most common type of motion for a wheel.
Translation
The wheel moves linearly, changing its position in space without rotating. This is often referred to as “rolling” when the wheel is in contact with a surface.
Combined Motion
The wheel can also undergo both rotation and translation simultaneously. This is the most common scenario for a wheel in motion, such as a car tire or a bicycle wheel.
Forces Acting on the Wheel
Several forces can act on a wheel, influencing its motion and behavior. Here are some key forces:
- Gravity: This force acts on the wheel’s mass, pulling it towards the center of the Earth. It influences the wheel’s weight and how it interacts with surfaces.
- Normal Force: This force acts perpendicular to the surface the wheel is in contact with, counteracting the force of gravity. It prevents the wheel from sinking into the surface.
- Friction: This force acts parallel to the surface, opposing the motion of the wheel. It can be static friction, preventing the wheel from moving initially, or kinetic friction, resisting the wheel’s movement while it is rolling.
- Applied Force: This is the force applied to the wheel, causing it to move or rotate. This force can be applied by a motor, a person pushing, or other external means.
- Air Resistance: This force opposes the wheel’s motion through the air, becoming more significant at higher speeds.
Relationship Between Radius, Angular Velocity, and Linear Velocity, A wheel of radius r and negligible mass is mounted
The relationship between a wheel’s radius, angular velocity, and linear velocity is fundamental to understanding its motion. Here’s a detailed explanation:* Angular Velocity (ω): This is the rate at which the wheel rotates, measured in radians per second (rad/s). It represents how quickly the wheel spins around its axis.
Linear Velocity (v)
This is the speed at which a point on the wheel’s circumference moves, measured in meters per second (m/s). It represents how fast the wheel is moving in a straight line.
Radius (r)
This is the distance from the center of the wheel to its outer edge, measured in meters (m).
The relationship between these quantities is:v = ωr
This equation shows that the linear velocity of a point on the wheel’s circumference is directly proportional to the angular velocity and the radius of the wheel. A larger radius or a faster angular velocity will result in a higher linear velocity.
As we conclude our journey with the wheel of radius r and negligible mass, we’ve uncovered a world of insights into the principles of motion, energy, and forces. From understanding the relationship between the wheel’s radius and its potential energy to recognizing how work done on the wheel translates into energy changes, we’ve gained a deeper appreciation for the fundamental mechanics at play.
This seemingly simple wheel, devoid of its own weight, serves as a powerful tool for visualizing and comprehending the intricate workings of the physical world. Its applications extend beyond the realm of theoretical exploration, finding relevance in real-world scenarios like pulleys, gears, and roller bearings. By understanding the behavior of this idealized wheel, we gain valuable insights into the design and optimization of complex mechanical systems.
Questions and Answers
What are some real-world examples of objects that can be approximated as a wheel with negligible mass?
Examples include pulleys in simple machines, gears in transmissions, and roller bearings in machinery. These objects are designed to minimize their own mass while maximizing their functionality in transmitting motion and forces.
How does the concept of a wheel with negligible mass apply to the real world?
While no real-world object is truly massless, the concept of negligible mass is a useful approximation in many situations. For example, when analyzing the motion of a pulley system, the mass of the pulley itself is often negligible compared to the masses of the objects being lifted. This allows for simplified calculations and a better understanding of the system’s overall behavior.